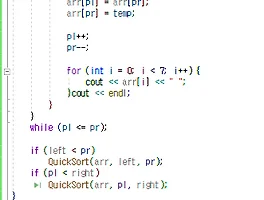
2. Manually determine the pairs of you who have the same birthday. Explain your method of solution.
1. 100명의 학생의 생일데이터를 다운로드합니다.
2. 다운받은 학생들의 생일 데이터를 오름차순으로 정렬합니다.
3. 오름차순으로 정렬한 생일 데이터를 사용하여 생일 같은 한 쌍의 학생이 있는지 확인합니다.
4. 01.19 , 01.20 , 02.07 , 03.09 , 03.28 , 04.28 , 05.18 , 06.16 , 07.19 , 08.02 , 09.05 , 09.25 , 10.19 , 11.15, 12.29 으로 총 15쌍의 학생들의 생일이 같다는 것을 확인할 수 있습니다.
4. Create code that calculates the probability of having at least two students with the same birthday in a class of k students. Apply several different ks.

위의 코드는 k명의 학생으로 구성된 반에서 생일이 같은 학생이 두 명 이상 있을 확률을 계산하는 코드입니다.
5. Demonstrate that if there are 100 students in a classroom, it is 99.999% probable that there is a pair of students with the same birthday. Conduct computational experiments to solve this problem.
a. Describe the algorithm in words as a verbal description.
k명의 학생으로 구성된 반에서 생일이 같은 학생이 두 명 이상 있을 확률은 1 - (365! / (365-k)!*365^k)의 식으로 구할 수 있다.
b. Show its correctness before you do coding. Use inductive proof.
k에 1을 대입하면 0.0이 나온다.

k에 23을 대입하면 0.507..이 나온다.

e. Develop the code to solve the problem
f. Show the results.
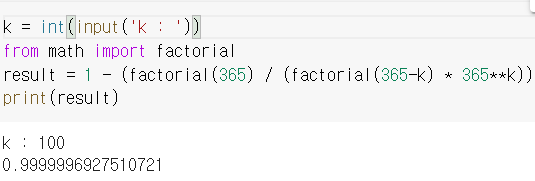
e. k에 100을 대입하여 한 교실에 100명의 학생이 있을 경우 생일이 같은 한 쌍의 학생이 있을 가능성이 0.999%임을 증명하였습니다.